2 posts tagged with "Power Analysis"

TL;DR​

• This blog post demonstrates how to deal with treated observations in sequential GeoLift testing.
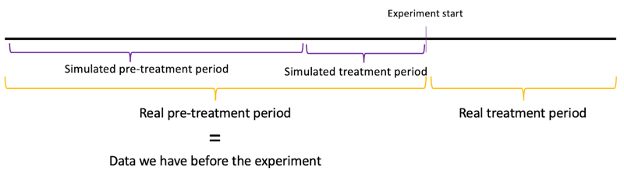
• Currently, when running two sequential GeoLifts, the treatment period of the first experiment becomes part of the pre-treatment period of the second experiment, potentially affecting results and power calculations.
• To prevent this, you can replace the treatment locations in the first experiment with the best counterfactual available. Once the treatment location has been replaced, make sure to expand the control donor pool with said series.
• We introduce our ReplaceTreatmentSplit function to replace the treated location units, easily implementing our proposed solution.

Introduction​

Advertisers have many questions to answer like, “What’s the incremental impact of this media channel?” and “What’s the budget elasticity of my investment in this channel?”. These questions and more can be answered using GeoLift.

Since each question is different and we cannot answer them all at the same time, we need to decide which of them we should answer first by building a learning agenda. Our agenda holds everything from business questions and hypotheses to specific experiment designs that will give us the answers we are looking for. For the sake of simplicity, imagine we have two business questions, and we run our first GeoLift (experiment 1) to answer the first one and would like to design a new GeoLift (experiment 2) to give an answer to our second inquiry.

However, running a second GeoLift immediately after the previous one is not that simple.

Sequential GeoLift testing​

At a first glance, we have a couple of options:

Option 1: Repeating our experiment 1 treatment group in experiment 2, excluding the experiment 1 periods.​

This implies that we will remove experiment 1 time periods from the pre-treatment period, meaning we will get the same time series we had before experiment 1 was run. Furthermore, if we rerun the power analysis with this series, we will get the same treatment group we had for experiment 1.

While an attractive option, it lacks flexibility due to the fact that we will probably choose the same treatment we did before experiment 1. Furthermore, we should make sure that the GeoLift model is able to accurately predict the most recent time-stamps, using the latest market dynamics. For example, if we had a test for all of December, then the model trained up to November might struggle to predict January due to different spending trends. Moreover, if the treatment was very long, this might make it very hard to justify tying the set of pre-treatment periods for experiment 1 to the periods during experiment 2.

Option 2: Rerunning the power analysis for experiment 2, without excluding experiment 1 periods.​

Without removing the periods from experiment 1, we will preserve the autocorrelation within the time series and avoid the sudden change that may occur, while keeping the latest time-stamps. Having said this, going with this option poses another threat. Locations that were used as a treatment group in experiment 1 will probably not be chosen as a good setup in the GeoLift ranking algorithm. When we run simulations using those locations, the simulated effect will probably be far off from the observed effect, since they already had a previous treatment that we are not considering.

If the locations selected as the treatment group presented a good setup for experiment 1, then at least some of them should be selected to be part of the treatment of experiment 2.

Our solution: Replace treatment group values from experiment 1​

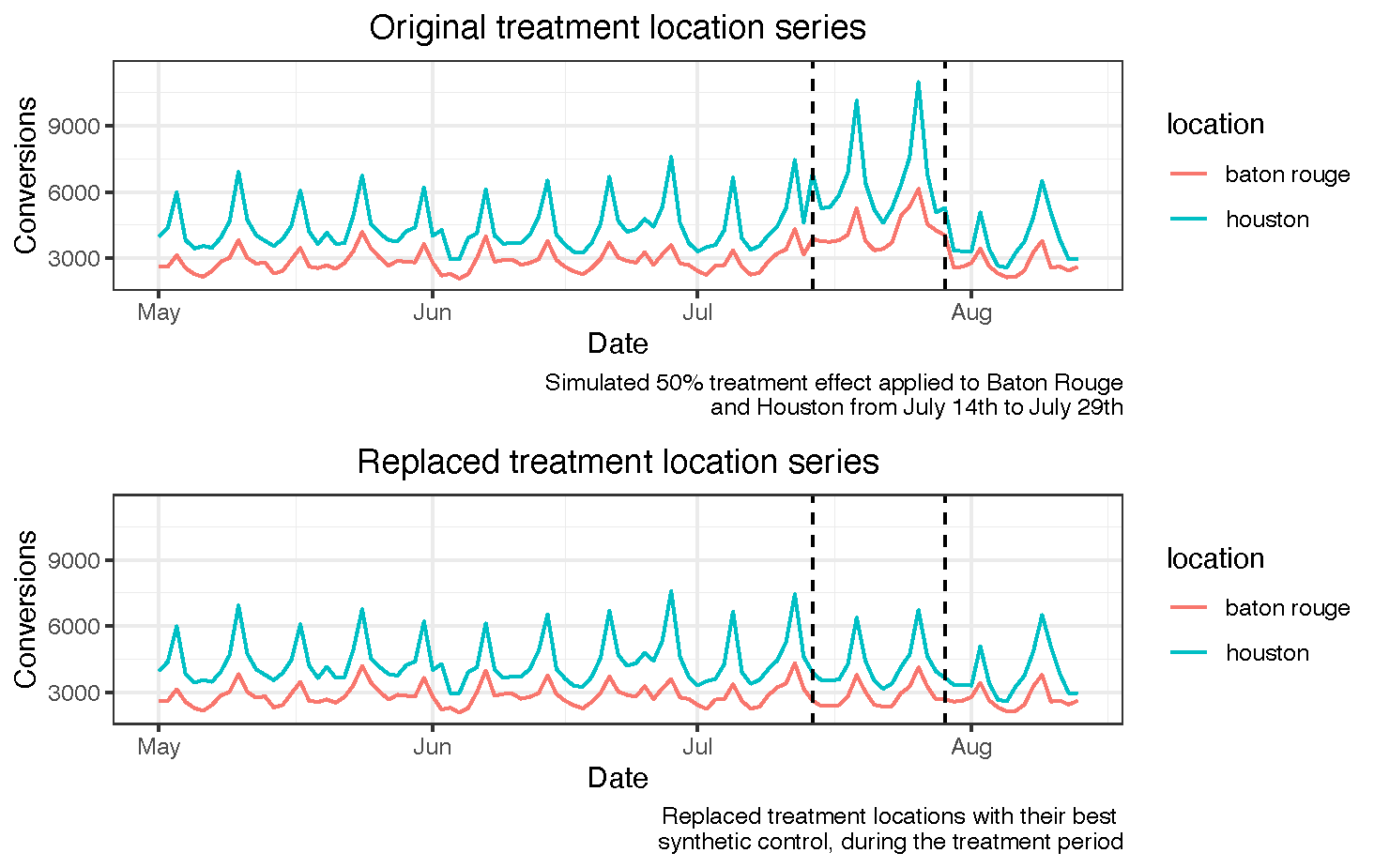
Our goal is maximizing the amount of data we have without excluding any periods and guaranteeing that our dataset does not contain any structural changes (treatment applied to certain locations in experiment 1). To do so, we recommend replacing the values of the locations that were treated during experiment 1, during the periods in which the treatment occurred and including them in the control donor pool. For reference, here’s a picture of what this looks like.

Here’s an example of our pseudo-code:

1. Define locations that were treated and treatment period during experiment 1.
2. Fit a GeoLift counterfactual to each of the treatment locations, training it on experiment 1’s pre-treatment period.
3. Only keep the counterfactual that has the closest match to a treatment location in the pre-treatment period (using absolute L2 imbalance, A.K.A. the sum of squared differences between treatment and control prior to the experiment).
4. Replace the selected treatment location by its counterfactual values during the experiment 1’s treatment period.
5. Reassign the replaced treatment location to the control donor pool.
6. Repeat this process until there are no more treatment locations left.

This solution has three clear benefits:

• We preserve the time series structure without excluding any data.
• We replace the structural change in the treatment locations by our best estimate of what would have happened if they had not been treated.
• We have a higher chance of providing better counterfactual fits for the replaced treatments because we are enlarging the control donor pool with each replacement.

Data-driven validation​

The last of these benefits does not necessarily mean that we will always be better off. Particularly, the algorithm will provide the same L2 imbalance values for cases where we have a smaller treatment size given that the added value of the replaced treatment to the control donor pool will not be as large.

In order to understand what was the average impact that our algorithm had on L2 imbalance, we decided to run a random selection of locations to build different treatment groups of 5 locations. We then passed those random groups through the algorithm, and compared it to the L2 imbalance that the counterfactual would have if the replaced treatment had not been added to the control donor pool. That is what we call the L2 imbalance improvement ratio:

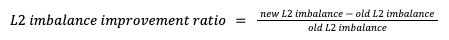
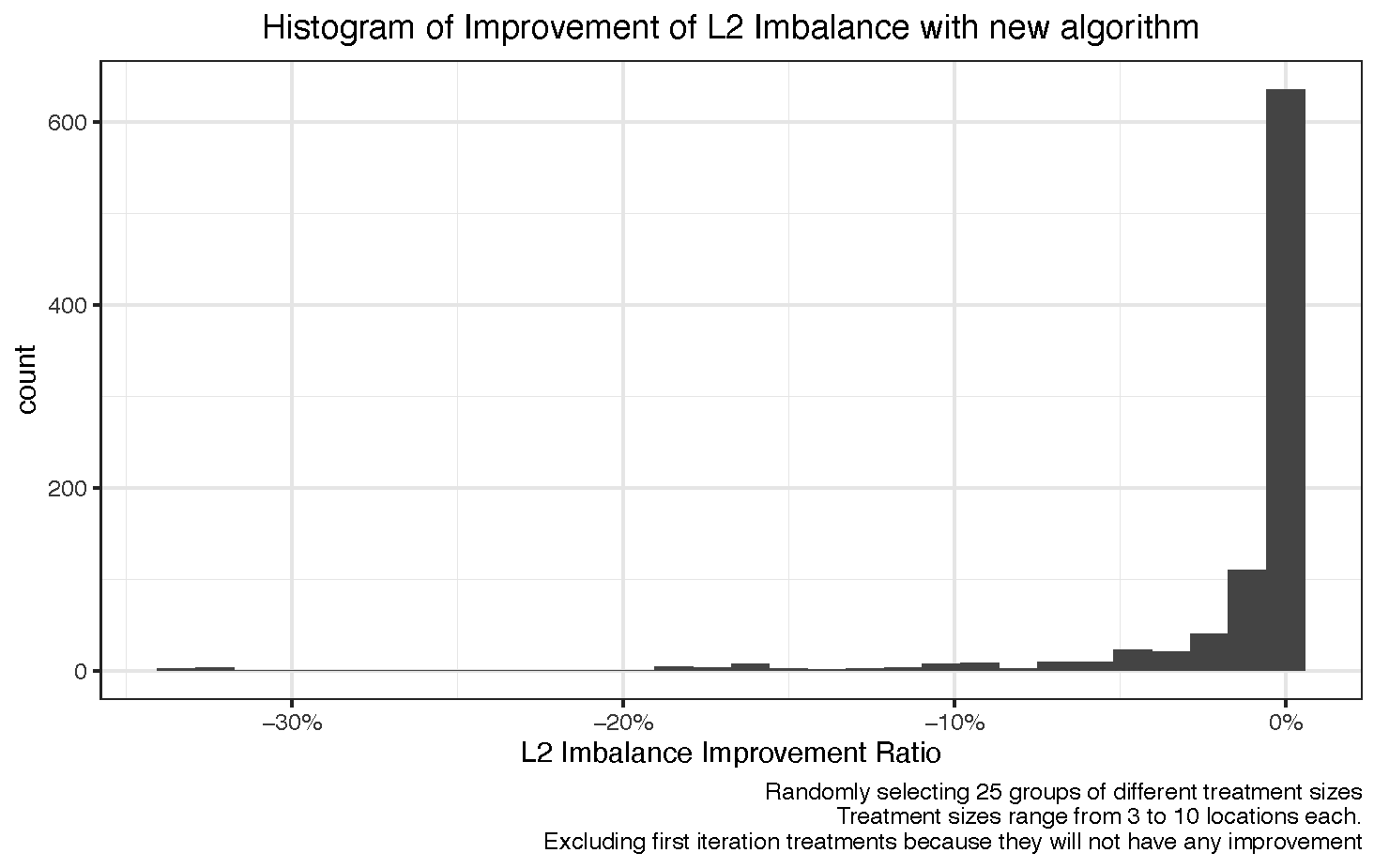
While the majority of the observations for the L2 imbalance improvement ratio are close to zero, there is a negative long tail that shows that there are some cases where our algorithm works better than the alternative.

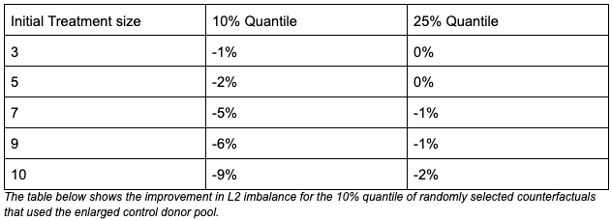
To make our finding more robust, we repeated the simulations with randomly selected treatment groups of different sizes. Looking at the 10% and 25% quantiles of the histogram provided above for each treatment size, we saw improvements in L2 imbalance of up to 8% in the 10% quantile. Naturally, the larger the treatment group, the higher the benefit of our proposed solution, in line with our aforementioned hypothesis.

How to implement the algorithm?​

We have recently landed a simple method for you to use if you would like to leverage this algorithm. Simply implement the ReplaceTreatmentSplit function, specifying what the treatment locations and the treatment start date and end date for experiment 1 are. You can pick up the replaced dataset from the $data argument in the list. The $l2_imbalance_df will give you the data frame of L2 imbalances for each treatment location when they were replaced.

# Import libraries and transform data.
library(GeoLift)
data(GeoLift_Test)
geo_data <- GeoDataRead(data = GeoLift_Test,
                        date_id = "date",
                        location_id = "location",
                        Y_id = "Y",
                        X = c(), #empty list as we have no covariates
                        format = "yyyy-mm-dd",
                        summary = TRUE)
treatment_group <- c(‘chicago’, ‘portland’)

# Replace treatment locations for best counterfactual.
g <- ReplaceTreatmentSplit(
  treatment_locations = treatment_group,
  data = geo_data,
  treatment_start_time = 90,
  treatment_end_time = 105,
  model = "none",
  verbose = TRUE
)

# Extract replaced data.
new_geo_data <- g$data

What’s up next?​

Keep your eye out for our coming blog posts, around topics like:

• When should I use Fixed Effects to get a higher signal to noise ratio?
• Long term branding measurement with GeoLift.

TL;DR​

• The success of a geo-based experiment greatly depends on the Market Selection process.
• In the GeoLift package, we use historical data and a simulation-based approach to identify the best set of treatment and control locations based on the constraints specified by the user.
• Selecting an appropriate value for the lookback_window parameter (the amount of pre-treatment periods that will be considered) is a very important part of the process.
• Based on the analysis presented in this note, we generally recommend using 1/10th of the pre-treatment period as a simulation lookback_window (especially if your time-series has a lot of variability across time).

What is considered a simulation in GeoLift?​

Essentially, before running the actual test, we are running a series of geo experiments to determine which is the best setup that will pave the way to success. As explained in further detail in our Blueprint Course, the GeoLift Market Selection process simulates a large number of geo experiments to determine which is the best test and control setup for you.

In each simulation a treatment effect is applied over a treatment group during the treatment period. Then, GeoLift then trains a counterfactual for the treatment group by using all of the pre-treatment periods prior to the experiment to assess the model's performance. Let’s breakdown each of these five components:

• The treatment effect: is the Lift percentage that will be applied to a set of locations during the testing period.
• The treatment group: these are a set of locations that will be exposed to the treatment effect.
• The counterfactual: these are a set of locations that are used to estimate what would have happened to the treatment group if it had not been exposed to the treatment effect. An easy way to think about it is as a weighted average of all the locations that are not part of the treatment group.
• The treatment period: represents the moments in which the treatment group will be exposed to the treatment.
• The pre-treatment period: this refers to the amount of periods that will be used to build the counterfactual, where there was no simulated difference between locations. During this period, the counterfactual and the treatment group should have a similar behavior.

Applying different effects to the same group in the same period allows us to holistically determine what the Minimum Detectable Effect (MDE) for that setup will be. Among other metrics, this helps us understand whether we are dealing with a combination of locations that will have a higher likelihood of observing small effect sizes. However, seasonalities and variations throughout time make can difficult to estimate the MDE with complete certainty. Fortunately, we can reduce this uncertainty by taking a look at the past!

Introducing the lookback window parameter.​

Our first simulation uses the most recent/latest periods in our series as our treatment period and all of the remaining periods as our pre-treatment period. This gives us the metrics we need to rank treatment groups for those time periods.

As stated in our GeoLift Walkthrough, we can increase the number of simulated time periods by changing the lookback_window. The lookback_window indicates how far back in time the simulations for the power analysis will go. By increasing the lookback_window, we subtract the last period from the previous simulation’s total duration and repeat the process over the remaining periods. Finally, we calculate the average metrics for each treatment group over all of the runs in different periods.

For example, imagine we have a 90 day long series with different locations and we would like to simulate a 15 day test, with a 2 day lookback_window.

• In the first simulation, the treatment period is made up of the most recent dates and Lift is simulated on it. The remainder, the pre-treatment period, is used to build a counterfactual. So, with a test duration of 15 days, for this iteration we use periods 1 to 75 as a pre-treatment period and periods 76 to 90 as a treatment period.
• For our second simulation, the treatment period is shifted by one timestamp. We use periods 1 to 74 as a pre-treatment period and periods 75 to 89 as a treatment period.
• We then construct average metrics per each treatment group, using these two simulations. In essence, we are repeating this flow until the number of time periods shifted is equal to the lookback_window parameter.

In this context, more simulations allow us to have a more robust estimate of the metrics for each treatment group, observing if the same behavior occurs across different simulated treatment and pre-treatment periods. The intuitive idea here is that we would like to capture some of the variability in the time series in our test setups, to avoid assuming something that could be different in the future.

There’s a tradeoff: robustness vs preciseness​

The more we look back into the past, the more simulations per treatment group we will have. This will make our estimates more robust and allow us to make safer predictions with regard to the pre-test metrics.

However, the more we look back into the past, the less precise our simulation will be as compared to the actual result. Removing the last periods we have prior to the test leads to two major effects:

• Our simulations become less precise because they have a smaller amount of periods to build the counterfactual than what the actual experiment will have.
• The accuracy of our simulation will be reduced since we are shortening the time that is being considered by the algorithm’s pre-treatment period.

Given this tradeoff, we need to choose the amount of simulations we run considering the potential they have but keeping in mind that they also have a downside. Moreover, it is important to note that incresing the lookback_window parameter will exponentially increase the number of simulations performed in the Market Selection algorithm and will result in a longer runtime.

How to choose the best lookback_window?​

The best way to analyze this problem is to capture the variance of detected effects in the same simulated treatment period for different treatment group combinations.

We have run this analysis using the dummy dataset that is available within the GeoLift package (data(GeoLift_PreTest)). This dataset is similar to the example we showed above: it has a total of 90 days of pre-experiment data, and we will simulate a test that will last 15 days. If we assume that there was no preexisting difference between locations, then the median of detected effects for each test start period should be around zero, which is the true effect.

The plot on the left shows the standard deviation of the detected effect per treatment start period. The plot on the right shows the range of detected effects for different treatment groups.

As we can see from the plot in the left, the standard deviation of the detected effect has a continuous drop from period 67 onwards. From the second plot, we can also observe that the median effect is close to zero, especially in the last periods.

Putting it in practice​

Since we have 75 pre-treatment periods in total, and the drop in standard deviation occurs in period 67, we would set a lookback_window of 8 periods.

To be as efficient as possible, we suggest running the GeoLiftMarketSelection function to find the best combination of markets with a lookback_window=1. With those best candidates, do a deep dive with a longer lookback_window=8 for each treatment combination by running GeoLiftPower, plot and analyze their power curves.

In conclusion​

The lookback_window parameter is a fundamental element of a robust Power Analysis and Market Selection. As a best practice, we recommend running a data-driven analysis similar to the one that was showcased here to identify the ideal value for this parameter. Alternatively, a great rule of thumb is to keep 1/10 of the pre-treatment periods for simulations, once the test duration has been defined. So, if you have a total of 150 periods before your experiment, and you want to run a 10 day test, a total of 140 pre-treatment periods would remain. Following this rule, you would have to set a lookback_window=14 for the preferred options that come out of the GeoLiftMarketSelection ranking.

At the very least, we suggest setting the lookback_window to a value that is at least as large as the time-series’ most granular seasonality (if we observe that sales vary widely throughout the days of the week, then setting the lookback_window to 7 would be a good start).

What’s up next?​

Stay tuned for our next blog posts, related to topics like:

• When should I use Fixed Effects to get a higher signal to noise ratio?
• When should our GeoLift test start?